Dipole field
Ok, so as an undergrad we calculate dynamics of charged particles in external electric fields. We might ask the question,"How did the motion of the particle affect the source of the field that caused the particle's motion?". To approach this dillema, a first idea is just have two particles near each other such that the motion of the particle is actually the motion of the field too. In classical electrodynamics, the particles are points and this two body system is soluble even analytically in some cases. For quantum systems, the two particle problem becomes much more difficult. A common starting point is to solve the Schrodinger equation for particle 1 perturbed by a time-dependent external field whose source is from particle 2.
We begin by splitting up the Hamiltonian up into two parts, the first term representing particle 1, the second term indirectly representing particle 2.
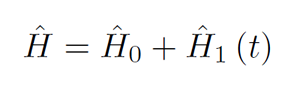
How does particle 1 stay locally bound with no other field sources(particles) to confine it? It is curious to note that the first term alone does indeed include a second particle in order for a bound state to be acheived. However, it is the second term that acts like a second particle interacting with the originally local single particle. The best way for me to interpret this is the single local particle 1 being a neutral atom treated as one particle with wave like behaviour.
Typically there are two schools of thought on this, are the differential equation approach, and the integral equation approach. Analytic dipole fields are not trivial at all, read this for more detail: Analytic approach to the dipole field.
back to Dynamic quantum states go to Nonreactive molecular collisions
