Reaction Dynamics

Molecular Collision Theory

Reaction dynamics is a field where approximation methods flourish. However, algebraic methods can be used to construct a Hamiltonian such that one may avoid differential operators and/or wave functions, thus avoid approximations. The familiar ladder operator form of the harmonic oscillator Hamiltonian is an example of this using a Lie algebra. When approaching molecular dynamics with this method the calculations become cleaner. A more common procedure, perturbation theory, results in an infinite amount of differential equations while the algebraic approach sustains analyticity with a finite amount of equations. However, the equations are coupled and nonlinear. To calculate dynamics of many atom systems, approximations are essential. Perhaps the most common approach is the Born-Oppenheimer Approximation. For processes with no electron transfer this method is analogous to the adiabatic theorem in that the nuclei move much slower than the electrons. The energy eigenvalue othe resulting equation is a function of the "parametrized" nuclear coordinates. This is considered the potential energy surface for the nuclei. This surface is available from electronic structure calculations or obtained by some semiempirical or emperical method. With this surface, reactions between different molecular species can be visualized intuitively. An important detail of these reactions is seen when different types of energy are transferred/exchanged during the scattering process...continue

Fundamental intermolecular interactions

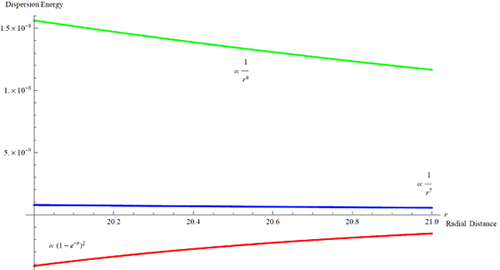
Here is a plot of a comparison between the Morse potential shape at large distances versus two other dispersion terms. It turns out that the red is only valid when two atoms are close, while farther out the green one becomes valid. Then even farther out recently it is shown that the blue shape is the true interatomic potential in the assymptotic region.

Computational applications

A discussion of vectors as instances of an algebra class leads to how easy it is for rotors to transform, dilate, rotate or reflect these vectors in their respective spaces with object oriented programming. I consider a new kind of product for two arbitrary multi-vectors. Using this goemetric product cleans up many derivations and representations in physics.  Here is a short look at what I am doing my dissertation on, Collisions.

Lie algebra is used to generate the quantum states of a molecule. A molecular Hamiltonian class is constructed by u(2) algebra class instances. Then a general total molecular state class is built with the Hamiltonian instances. Methods are used in the construction of normal and local modes of a given molecule with direct products of single algebra instances. Other methods are then used to raise and lower the stretching, rotational and bending quantum states of molecular instances. A clear example is then calculated for a tetrahedral molecule from the ground state gaining quanta in different forms. Here is a poster of the idea Object Oriented Approach to the Algebraic Theory of Molecules .

The major unique aspects of object oriented programming all stem from one key idea, inheritance.

• Inheritance

The idea of inheritance is simple but powerful: When you want to create a new class and there is already a class that includes some of the code that you want, you can derive your new class from the existing class. In doing this, you can reuse the fields and methods of the existing class without having to write (and debug!) them yourself. The advantages of inheritance are:

1. Abstraction

Abstraction is simplifying complex reality by modeling classes appropriate to the problem, and working at the most appropriate level of inheritance for a given aspect of the problem.

2. Data Encapsulation

Encapsulation conceals the functional details of a class from objects that send messages to it. Under this definition, encapsulation means that the internal representation of an object is generally hidden from view outside of the object's definition. Typically, only the object's own methods can directly inspect or manipulate its fields. Hiding the internals of the object protects its integrity by preventing users from setting the internal data of the component into an invalid or inconsistent state. A benefit of encapsulation is that it can reduce system complexity and thus increases robustness, by allowing the developer to limit the interdependencies between software components.

3. Interfacing

An interface is a reference type, similar to a class, that can contain only constants, method signatures, and nested types. There are no method bodies. Interfaces cannot be instantiated—they can only be implemented by classes or extended by other interfaces. For instance, a human and a parrot can both whistle; however, it would not make sense to represent Humans and Parrots as subclasses of a Whistler class. Rather they would most likely be subclasses of an Animal class (likely with intermediate classes), but both would implement the Whistler interface. All of the molecule's initial conditions and important parameters will be in an interface called parameters. In general, the interface concept in programing is a sort of specification that allows different entities to call and make use of the other, with the implication that the caller need not know what's behind the facade. Unlike interfaces, abstract classes can contain fields that are not static and final, and they can contain implemented methods. Such abstract classes are similar to interfaces, except that they provide a partial implementation, leaving it to subclasses to complete the implementation. If an abstract class contains only abstract method declarations, it should be declared as an interface instead.

4. Package

A package is a grouping of related types providing access protection and name space management. Note that types refers to classes, interfaces, enumerations, and annotation types. Enumerations and annotation types are special kinds of classes and interfaces, respectively, so types are often referred to in this lesson simply as classes and interfaces.

5. Polymorphism

In object-oriented programming, polymorphism refers to a programming language's ability to process objects differently depending on their data type or class. More specifically, it is the ability to redefine methods for derived classes. For example, given a base class shape, polymorphism enables the programmer to define different area methods for any number of derived classes, such as circles, rectangles and triangles. No matter what shape an object is, applying the area method to it will return the correct results.

In application to molecular collisions

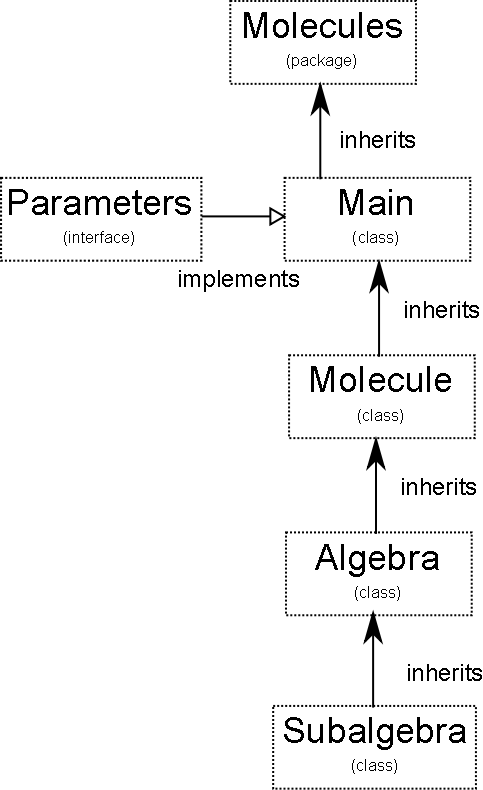
I am using objects to minimize the size of actual code to debug during an explicit calculation. The process can be seen graphically below:

Key Processes: The first inheritance at the bottom can be of a vector of subalgebra instances. The algebra class must then contain a method which combines subalgebra objects into larger algebra via a method of the algebra class called directProduct(). The second inheritance in the molecule is making use of a single algebra instance. A method is then written for the molecule class that allows a calculation of the amplitude  of any particular operator within the array of subalgebra instances. This can only be done because an instantiation of a molecule carries with it arbitrary fock space states. The third inheritance is in the main class which contains the explicit calculation formed from methods of its subclasses. The great advantage here is that knowing the subclasses are functioning properly I get to work with less code formed from fundamental objects at a "higher level". At this point the molecule class implements the parameters interface. This keeps the initial conditions and constant parameters associated with a calculation separate, simplifying the overall debugging process. Raise and Lower Molecule Methods correct to mode Set natural frequency and depth of Morse Get Spectrum and threshold for dissociation Get State Get Transition Amplitudes Write collide method Write normal or local mode algebra construction method

download Molecular collision Net Beans project